7. DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法。基于密度的聚类算法一般假定类别可以通过样本分布的紧密程度决定,同一类别的样本是紧密相连的,也就是说,在该类别任意样本周围不远处一定有同类别的样本存在。
将紧密相连的样本划为一类,这样就得到了一个聚类类别;通过将各组紧密相连的样本划为多个不同的类别,就得到了最终的聚类结果。
7.1. 概念
参数对 ( \(\epsilon\) , \(MinPts\) ) 用来描述邻域的样本分布紧密程度,\(\epsilon\) 是样本的邻域距离阈值,\(MinPts\) 是邻域中样本个数的阈值。
假设有样本集 \(\mathcal{D} = \{ x_1, x_2, \cdots, x_n \}\) ,定义几个概念如下:
\(\epsilon\) 邻域(Eps-Neighborhood):\(\mathcal{N}_{\epsilon}(x_i) = \{ x_j \in \mathcal{D} | \mathrm{distance}(x_i, x_j) \leq \epsilon \}\) 。
核心点(Core Points):核心点的 \(\epsilon\) 邻域包含至少 \(MinPts\) 个样本点。
密度直达(Directly Density-Reachable):假设 \(x_i\) 是核心点,\(x_j \in \mathcal{N}_{\epsilon}(x_i)\) ,则称 \(x_j\) 由 \(x_i\) 密度直达,反之不一定成立。
密度可达(Density-Reachable):假设存在样本序列 \(p_1, p_2, \cdots, p_T\) ,满足 \(p_1 = x_i, p_T = x_j\) ,且 \(p_1, p_2, \cdots, p_{T-1}\) 都是核心点, \(p_{t+1}\) 由 \(p_t\) 密度直达,则称 \(x_j\) 由 \(x_i\) 密度可达,反之不一定成立。
密度相连(Density-Connected): 对于 \(x_i\) 和 \(x_j\) ,如果存在核心点 \(x_k\) ,使 \(x_i\) 和 \(x_j\) 均由 \(x_k\) 密度可达,则称 \(x_i\) 和 \(x_j\) 密度相连;密度相连关系是满足对称性的。
7.2. 聚类思想
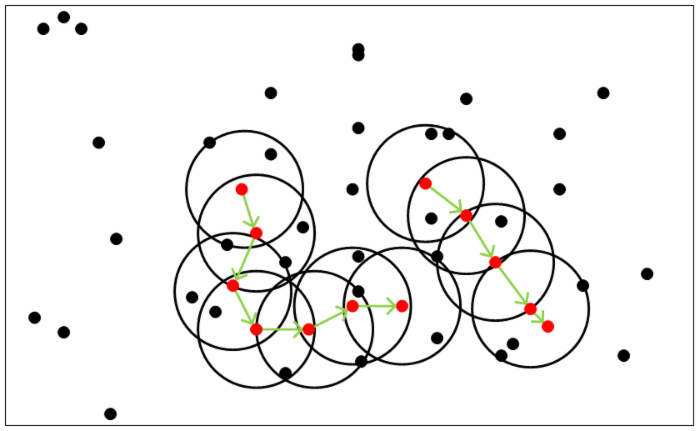
DBSCAN 的聚类思想很简单:由密度可达关系导出的最大密度相连的样本集合,即为最终聚类的一个类别/簇。
一个簇里面可以有一个或者多个核心点。如果只有一个核心点,则簇里其他的非核心点都在这个核心点的 \(\epsilon\) 邻域里;如果有多个核心点,则簇里的任意一个核心点的 \(\epsilon\) 邻域中一定有一个其他的核心点,否则这两个核心点无法密度可达。这些核心点的 \(\epsilon\) 邻域里的样本的集合组成一个簇。
DBSCAN 首先选择一个核心点作为种子,然后找到所有这个核心点能够密度可达的样本集合,即为一个聚类簇;接着继续选择另一个尚未访问过的核心点去寻找密度可达的样本集合,这样就得到另一个聚类簇。一直执行直到所有核心点都访问过为止。
还有三个问题需要注意:
存在一些异常样本点或者说少量游离于簇外的样本点(Outliers),这些点不在任何一个核心点的周围。
需要采用某一种距离度量来衡量样本距离,比如欧氏距离。对于少量的样本,寻找最近邻可以直接去计算所有样本的距离矩阵;如果样本量较大,则一般采用 K-D 树或者球树(Ball Tree)来快速搜索最近邻。
DBSCAN 不是完全稳定的算法,当某个样本到两个核心点的距离都小于阈值,但是这两个核心点不是密度直达,不属于同一个聚类簇,那么如果界定这个样本的类别呢?一般来说,DBSCAN 按照先来后到的原则,先访问到的核心点会先将这个样本归属到它的簇内。
DBSCAN 的优点:
可以对任意形状的稠密数据集进行聚类,而 K-Means 之类的聚类算法一般只适用于凸数据集(在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。例如,立方体是凸集,月牙形不是凸集)。
可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
聚类结果相对稳定。
不需要指定聚类的数量。
DBSCAN 的缺点:
如果样本集的密度不均匀、类内间距相差很大时,聚类质量较差。
如果样本集较大,聚类收敛时间较长,可以对搜索最近邻时建立的 K-D 树或者球树进行规模限制来改进。
需要对距离阈值 \(\epsilon\) 和邻域样本数阈值 \(MinPts\) 联合调参,不同的参数组合对最后的聚类效果有较大影响。
Note
Python 的 scikit-learn 包实现了 DBSCAN 算法,0.14 版本之前的实现需要计算样本间的距离矩阵,效率较低,新版本则使用了 K-D 树和球树进行了优化。
7.3. 算法流程
输入:样本集 \(\mathcal{D} = \{ x_1, x_2, \cdots, x_n \}\) ;参数对 ( \(\epsilon\) , \(MinPts\) )
输出:簇划分 \(\{ \mathcal{C}_1, \mathcal{C}_2, \cdots \}\)
算法流程
初始化:核心点集合 \(\mathcal{\Omega} = \emptyset\) ;聚簇数量 \(k = 0\) ;尚未访问的样本点集合 \(\mathcal{V} = \mathcal{D}\) 。
对于所有样本点 \(x_i \in \mathcal{D}\) ,计算其 \(\epsilon\) 邻域 \(\mathcal{N}_{\epsilon}(x_i)\) :
若 \(| \mathcal{N}_{\epsilon}(x_i)| \geq MinPts\) ,则加入核心点集合。
否则,先将其标记为噪声点(当噪声点位于某个核心点的邻域,后续会被分配到该核心点所属的簇中,否则该点就是离群点)。
WHILE( 核心点集合 \(\mathcal{\Omega}\) 不为空 ):
依次选择一个核心点 \(o\),建立当前核心点队列 \(\mathcal{Q}_k = \{o\}\) ;更新簇个数 \(k = k+1\) ;建立当前簇集合 \(\mathcal{C}_k = \{o\}\) 。
WHILE( 当前核心点队列 \(\mathcal{Q}_k\) 不为空 ):
从 \(\mathcal{Q}_k\) 中出队一个核心点 \(o^{\prime}\) ,把 \(\mathcal{N}_{\epsilon}(o^{\prime})\) 加入当前簇集合 \(\mathcal{C}_k\) ,同时需要更新未访问的样本点集合 \(\mathcal{V}\) ;将 \(\mathcal{N}_{\epsilon}(o^{\prime})\) 中属于核心点的样本点加入队列 \(\mathcal{Q}_k\) 。
7.4. 参考资料
Clustering
DBSCAN密度聚类算法
A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise
Visualizing DBSCAN Clustering