2. 支持向量机

2.1. 最大间隔划分超平面

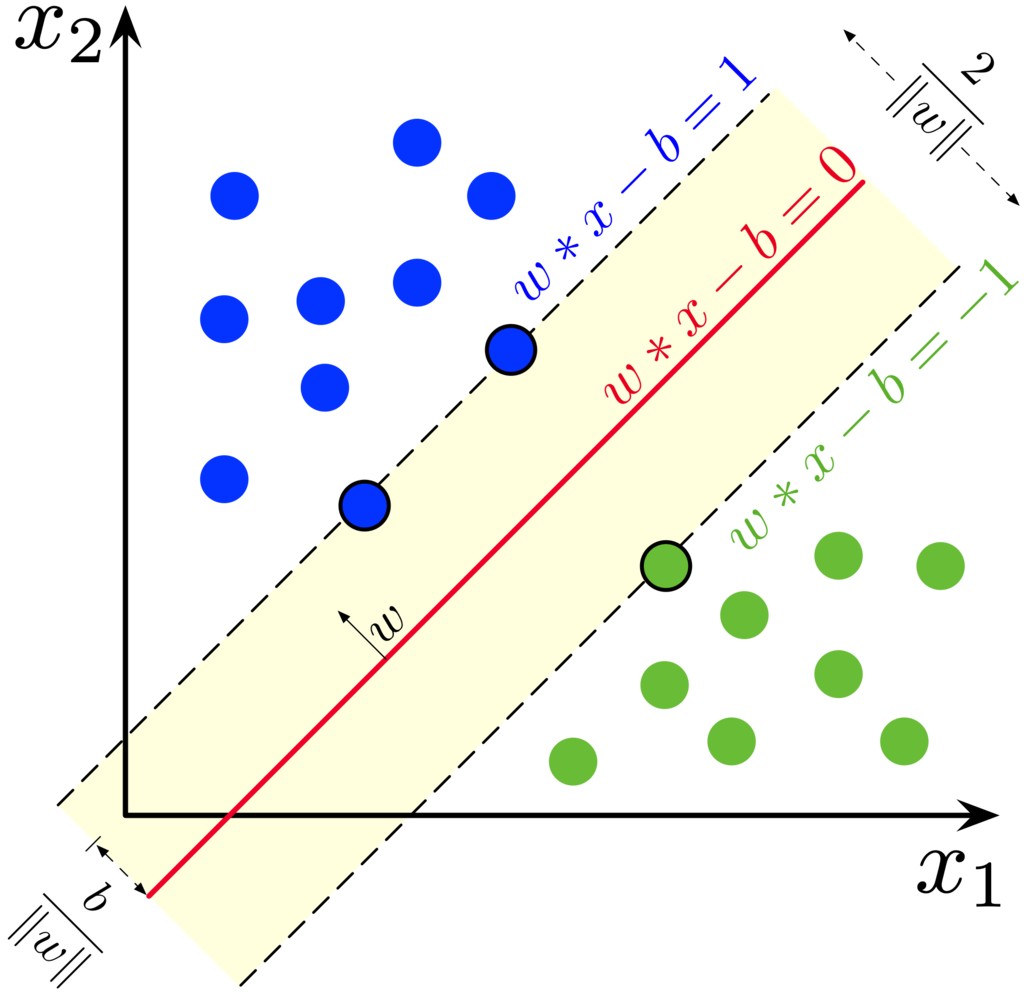
../_images/02_margin.png

样本空间中任意点到超平面的距离（几何间隔，Geometric Margin）为：

\[r = \frac{|w^{\top} x + b|}{\| w \|}.\]

函数间隔（Functional Margin）：

\[y(w^{\top} x + b).\]

原始问题：

\[\begin{split}\underset{w,b}{\mathrm{min}} &\ \frac{1}{2} \left \| w \right \|^2 \\ \mathrm{s.t.} &\ y_i(w^{\top} x_i + b) \geqslant 1, i=1,2,...,m\end{split}\]

拉格朗日函数：

\[L(w,b,\alpha) = \frac{1}{2}w^{\top}w + \sum_{i=1}^m \alpha_i(1 - y_i(w^{\top} x_i + b))\]

目标函数：

\[\underset{w,b}{\mathrm{min}}(\underset{\alpha \geqslant 0}{\mathrm{max}}L(w,b,\alpha))\]

对偶问题：

\[\underset{\alpha \geqslant 0}{\mathrm{max}}(\underset{w,b}{\mathrm{min}}L(w,b,\alpha))\]

令 \(L\) 对 \(w\) 和 \(b\) 的偏导为 0 得：

\[\begin{split}w &=\ \sum_{i=1}^m \alpha_i y_i x_i,\\ 0 &=\ \sum_{i=1}^m \alpha_i y_i.\end{split}\]

对偶问题变成：

\[\begin{split}\underset{\alpha \geqslant 0}{\mathrm{max}} & \ \sum_{i=1}^m\alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j x_i^{\top} x_j,\\ \mathrm{s.t.} & \ \sum_{i=1}^m \alpha_i y_i = 0,\\ & \ \alpha_i \geqslant 0, \ i=1,2,...,m.\end{split}\]

KKT条件：

\[\begin{split}y_i(w^{\top} x_i + b) \geqslant 1, \\ \sum_{i=1}^m \alpha_i y_i = 0,\\ \alpha_i (1 - y_i(w^{\top} x_i + b)) = 0.\end{split}\]

2.2. 软间隔

引入松弛变量 \(\xi_i \geqslant 0\) ，用以表征样本不满足约束的程度。

原始问题：

\[\begin{split}\underset{w,b,\xi_i}{\mathrm{min}} &\ \frac{1}{2} \left \| w \right \|^2 + C \sum_{i=1}^m \xi_i \\ \mathrm{s.t.} &\ y_i(w^{\top} x_i + b) \geqslant 1 - \xi_i \\ &\ \xi_i \geqslant 0,\ i=1,2,...,m\end{split}\]

拉格朗日函数：

\[L(w,b,\alpha,\xi,\mu) = \frac{1}{2}w^{\top}w + C \sum_{i=1}^m \xi_i + \sum_{i=1}^m \alpha_i(1 - \xi_i - y_i(w^{\top} x_i + b)) - \sum_{i=1}^m \mu_i \xi_i\]

令 \(L\) 对 \(w\) ， \(b\) 和 \(\xi_i\) 的偏导为 0 得：

\[\begin{split}w &=\ \sum_{i=1}^m \alpha_i y_i x_i,\\ 0 &=\ \sum_{i=1}^m \alpha_i y_i, \\ C &=\ \alpha_i + \mu_i.\end{split}\]

对偶问题：

\[\begin{split}\underset{\alpha \geqslant 0}{\mathrm{max}} & \ \sum_{i=1}^m\alpha_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j x_i^{\top} x_j,\\ \mathrm{s.t.} & \ \sum_{i=1}^m \alpha_i y_i = 0,\\ & \ 0 \leqslant \alpha_i \leqslant C, \ i=1,2,...,m.\end{split}\]

KKT条件：

\[\begin{split}y_i(w^{\top} x_i + b) \geqslant 1 - \xi_i, \\ \sum_{i=1}^m \alpha_i y_i = 0,\\ \alpha_i (1 - \xi_i - y_i(w^{\top} x_i + b)) = 0, \\ \xi_i \geqslant 0,\ \mu_i \xi_i = 0, \\ \alpha_i \geqslant 0,\ \mu_i \geqslant 0.\end{split}\]
惩罚因子 \(C\) ：

  • \(C\) 太大，导致过拟合（低偏差、高方差）

  • \(C\) 太小，导致欠拟合（高偏差、低方差）

2.3. 核函数

核矩阵 \(\mathcal{K} = \{ \kappa(x_i, x_j) \} \in \mathbb{R}^{m \times m}\) 。

  • 核矩阵对称半正定，\(\mathcal{K} \geqslant 0: \forall z,\ z^{\top}\mathcal{K}z \geqslant 0;\) \(z^{\top}\mathcal{K}z=0\) 当且仅当 \(z=0\) 。

    \[\begin{split}z^{\top}\mathcal{K}z &=\ \sum_{i=1}^m \sum_{j=1}^m z^{(i)} \kappa(x_i, x_j) z^{(j)} \\ &=\ \sum_{i=1}^m \sum_{j=1}^m z^{(i)} \phi(x_i)^{\top} \phi(x_j) z^{(j)} \\ &=\ \sum_{i=1}^m \sum_{j=1}^m z^{(i)} \cdot \sum_{k=1}^D \phi^{(k)}(x_i)\phi^{(k)}(x_j) \cdot z^{(j)} \\ &=\ \sum_{i=1}^m \sum_{j=1}^m \sum_{k=1}^D z^{(i)} \phi^{(k)}(x_i) \cdot z^{(j)} \phi^{(k)}(x_j) \\ &=\ \sum_{k=1}^D \sum_{i=1}^m \sum_{j=1}^m z^{(i)} \phi^{(k)}(x_i) \cdot z^{(j)} \phi^{(k)}(x_j) \\ &=\ \sum_{k=1}^D \left( \sum_{l=1}^m z^{(l)} \phi^{(k)}(x_l) \right)^2 \\ & \geqslant \ 0.\end{split}\]

    其中上标 \((i),(j),(k),(l)\) 分别表示向量的第 \(i,j,k,l\) 维分量。当 \(\phi\) 维度很高，单独计算 \(\phi(x_i)\) 和 \(\phi(x_j)\) 复杂度较高， 而直接计算 \(\kappa(x_i, x_j)\) 则简单得多。

  • 常见核函数有：

    • 线性核：\(\kappa(x_i, x_j) = x_i^{\top}x_j\)

    • 多项式核：\(\kappa(x_i, x_j) = (x_i^{\top}x_j)^d\)

    • 高斯核：\(\kappa(x_i, x_j) = \mathrm{exp}(-\frac{\| x_i - x_j \|^2}{2 \sigma^2})\)

    • 拉普拉斯核：\(\kappa(x_i, x_j) = \mathrm{exp}(-\frac{\| x_i - x_j \|}{\sigma})\)

  • 主要使用线性核，高斯核（RBF）。

  • 当特征维度高且样本少，不宜使用高斯核，容易过拟合。

  • 当特征维度低，且样本够多，考虑使用高斯核。首先需要特征缩放（归一化）。若 \(\sigma\) 过大，导致特征间差异变小，欠拟合。

2.4. 多分类

  1. 一对一（ \(\mathcal{O}(N^2)\) ）

  2. 一对多（ \(\mathcal{O}(N)\) ）

  3. 使用多分类 Loss

2.5. SVM库

  • sklearn

  • libsvm

2.6. 优缺点

优点

  • 基于结构风险最小化，泛化能力强（自带正则化， \(\left \| w \right \|^2\) ）。

  • 它是凸优化问题，可得到全局最优。

  • SVM 在小样本训练集上可得到比其他方法好的结果。

  • 利用核函数，可借助线性可分问题的求解方法，直接求解对应高维空间的问题。

缺点

  • SVM 对缺失特征敏感。

  • 如何确定核函数？

  • 求解问题的二次规划，耗时耗存储。

2.7. 解析

  1. 为什么要间隔最大化？

最优超平面，解唯一，更加鲁棒。

  1. 为什么转化为对偶问题？

  • 便于求解（交换 \(\alpha\) 和 \((w,b)\) 位置之后，可直接对 \((w,b)\) 求导）。

  • 解的过程可以引入核函数。

2.8. SVM 与 LR 的异同

相同点：

  • 都是分类算法。

  • 不考虑核函数，分类面都是线性。

  • 都是监督学习算法。

  • 都是判别模型。（判别模型：KNN，SVM，LR；生成模型：HMM，朴素贝叶斯）

不同点：

  • 本质不同：Loss Function不同

  • SVM 只有支持向量影响模型，LR 中每个样本都有作用。

  • SVM 针对线性不可分问题有核函数。

  • SVM 依赖样本间的距离测度，样本特征需要归一化，也就是说 SVM 基于距离，LR 基于概率。

  • SVM 是 结构风险最小化 算法（在训练误差和模型复杂度之间的折中，防止过拟合，从而达到真实误差最小化），因为 SVM 自带正则（ \(\left \| w \right \|^2\) ）。

2.9. 参考资料

  1. LR与SVM的异同

  1. 核函数

  1. SVM面试题

  1. SVM的优缺点

  1. 机器学习技法–SVM的对偶问题

  1. 周志华《机器学习》Page 121 – 124。

  2. Support-vector machine

  1. 约束优化方法之拉格朗日乘子法与KKT条件

  1. 关于拉格朗日乘子法及KKT条件的探究