3. 主成分分析

PCA : Principal Component Analysis.

最大可分性 ：所有样本点到超平面的投影能尽可能分开（投影后样本点方差最大化）。

PCA 是一种正交线性变换，把数据变换到一个新的坐标系统中，把相关变量变换为不相关变量。

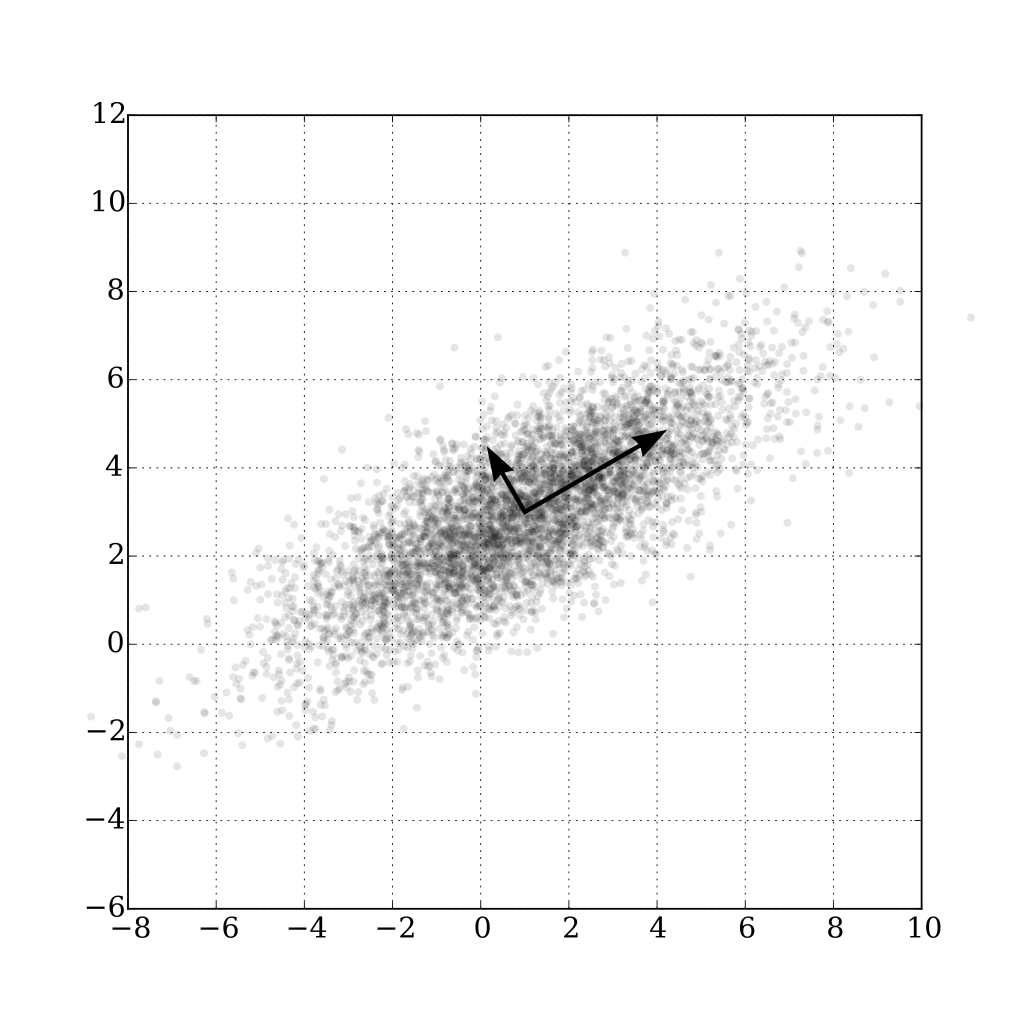
../_images/03_pca.png

3.1. 优化目标

样本点到超平面的投影为 \(W^{\top}X\) ，假设 \(X\) 已经中心化。

\[\begin{split}\underset{W}{\mathrm{max}} & \ Tr(W^{\top}XX^{\top}W) \\ s.t. & \ W^{\top}W=I. \\ & \ X \in \mathbb{R}^{d \times m}, \\ & \ W \in \mathbb{R}^{d \times d^\prime}, \\ & \ d^\prime < d.\end{split}\]

3.2. 推导

利用拉格朗日乘子法，

\[L = - Tr(W^{\top}XX^{\top}W) + \lambda (W^{\top}W - I),\quad \lambda \neq 0.\]

令 \(L\) 对 \(W\) 和 \(\lambda\) 的偏导为 0 得：

\[\begin{split}XX^{\top}W &=\ \lambda W, \\ W^{\top}W &=\ I.\end{split}\]

对协方差矩阵 \(XX^{\top}\) 进行特征值分解即可。

如何选择 \(d^\prime\) 个特征向量？

\(X\) 经过 \(w_j\) 投影后的方差为 \(w_j^{\top} X X^{\top} w_j = \lambda_j w_j^{\top} w_j = \lambda_j\) ， 即 \(XX^{\top}\) 的第 \(j\) 个特征值对应了样本投影后的第 \(j\) 个属性的方差。本着方差最大化的原则， 选取最大的 \(d^\prime\) 个特征值对应的特征向量。

3.3. 求解

  1. 样本中心化： \(X\) 减均值。

  2. 计算样本的协方差矩阵 \(C = XX^{\top}\) ；

  3. 对协方差矩阵做特征值分解（EVD）；

  4. 取最大的 \(d^\prime\) 个特征值 \((\lambda_1, \lambda_2,...,\lambda_{d^\prime})\) 对应的特征向量：

    \[W = (w_1, w_2,...,w_{d^\prime})\]

3.4. PCA-Whitening

白化（Whitening）的目的是降低输入的冗余性：

  • 特征之间相关性降低

  • 所有特征具有相同的方差

\[\begin{split}x_{rot} &=\ W^{\top} x, \\ x_{pca\ white, i} &=\ \frac{x_{rot, i}}{\sqrt{\lambda_i}}\end{split}\]

3.5. SVD分解

\[\begin{split}A &=\ U \Sigma V^{\top},\\ A & \in \mathbb{R}^{m \times n}, \\ r &=\ rank(A),\\ U & \in \mathbb{R}^{m \times r}, \\ \Sigma & \in \mathbb{R}^{r \times r}, \\ V & \in \mathbb{R}^{n \times r}.\end{split}\]

其中 \(U\) 是 \(AA^{\top}\) 的特征向量矩阵， \(V\) 是 \(A^{\top}A\) 的特征向量矩阵。

当 \(d\) 很大时， \(C=XX^{\top}\) 是很高维的矩阵，计算该矩阵并求特征向量开销大。此时对 \(X\) 做SVD分解，得到 \(U\) 便是 协方差矩阵 \(C\) 的特征向量。

Note

均值方差标准化（Standard Score Normalization，Z-Score Normalization）： \(z = \frac{x - \mu}{\sigma}\) ， 将原始数据转化为均值为 0、标准差为 1 的数据分布，减少不同维度的特征之间的尺度差异性，使其具有可比性，加速算法的收敛速度、提升精度。

3.6. 参考资料

  1. 周志华《机器学习》Page 229 – 232。

  2. ufldl