14. 称重问题
14.1. 一般解
已知条件 |
目标 |
\(n\) 次称重可解问题的规模(最大硬币数量) |
\(c\) 个硬币所需的最大称重次数 |
|---|---|---|---|
存在一个硬币比其他硬币轻(重) |
找到该硬币 |
\(3^n\) |
\(\lceil \log_3(c) \rceil\) |
存在一个硬币重量不一样 |
找到该硬币 |
\(\frac{3^n-1}{2}\) |
\(\lceil \log_3(2c+1) \rceil\) |
存在一个硬币重量不一样或所有硬币一样重 |
如果存在一个硬币重量不一样,找到它并判断轻还是重 |
\(\frac{3^n-1}{2}-1\) |
\(\lceil \log_3(2c+3) \rceil\) |
- 注:
给定 \(\frac{3^n-1}{2}\) 个硬币,\(n\) 次称重可以找到重量异常的硬币,但是不一定能判断该硬币是轻了还是重了。
给定 \(\frac{3^n-1}{2} - 1\) 个硬币,\(n\) 次称重一定可以找到重量异常的硬币,并判断该硬币是轻了还是重了。
- 例:
10 个硬币,存在 1 个硬币较轻,3 次称量可以找出该硬币。
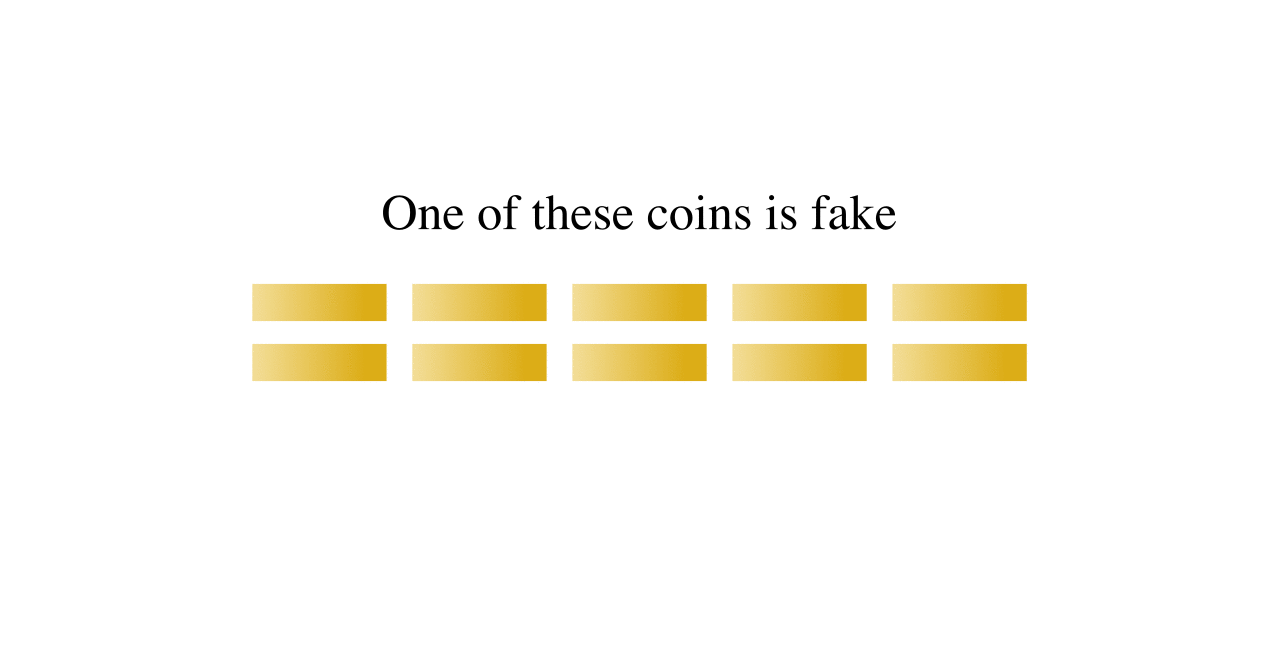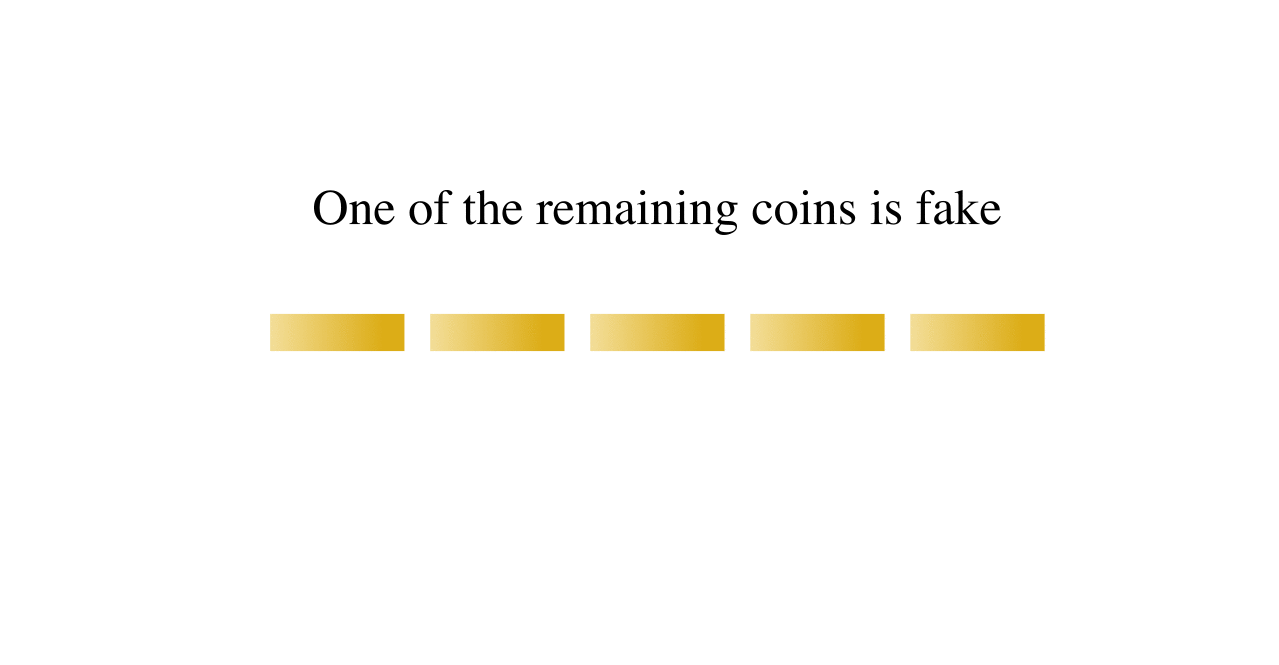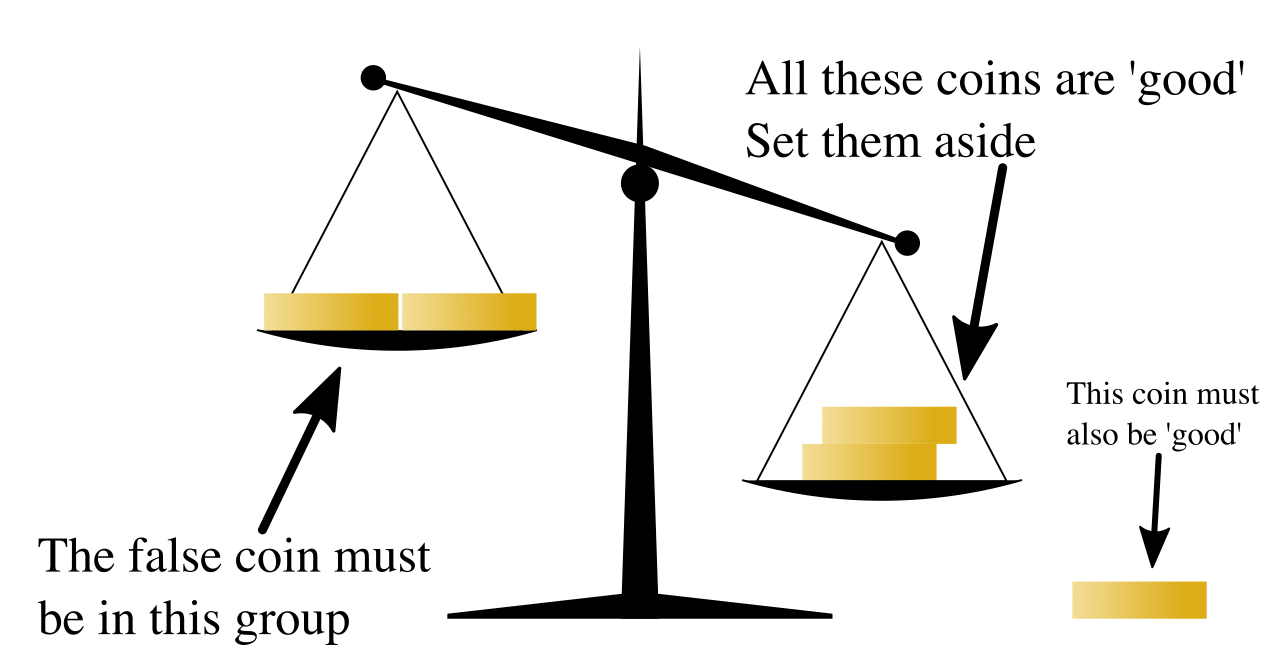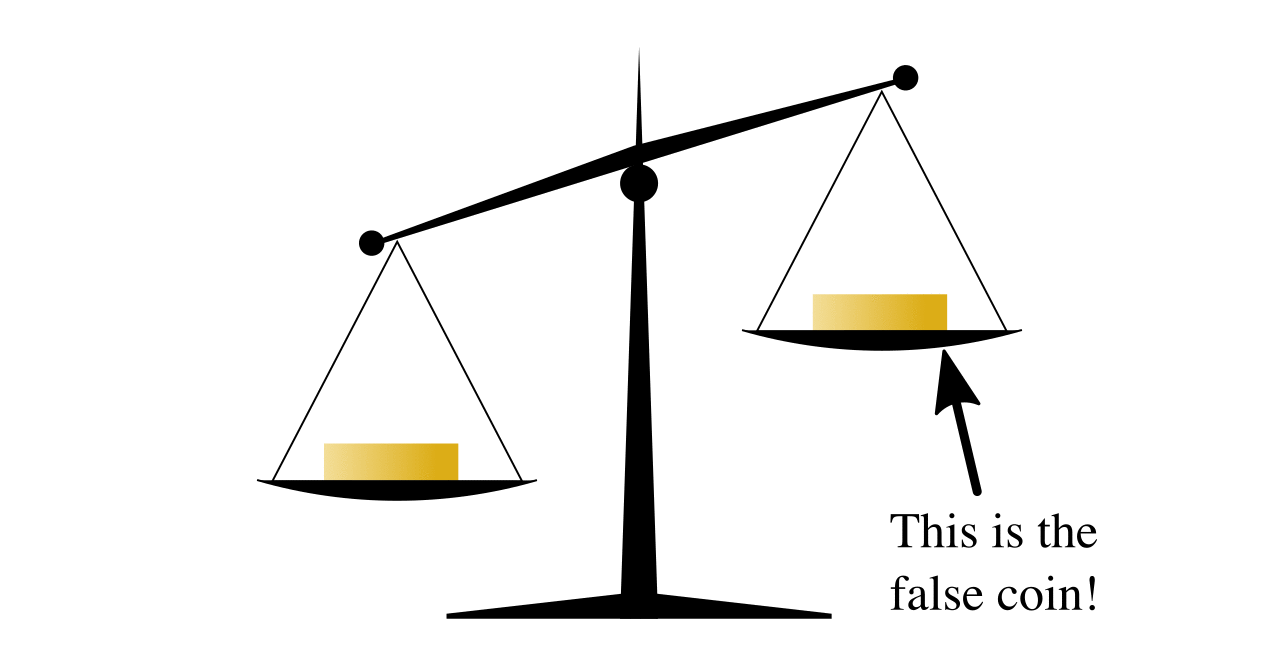
14.2. 8 硬币问题
存在一个硬币比其他硬币轻(重)
二分法,需要 3 次称量。
三分法,分组为(3,3,2),只需要两次称量。
存在一个硬币重量不一样
- 方法
Step 1. 把硬币按照下标分成三组:(1,2,3),(4,5,6),(7,8)。
Step 2. 比较第一组(1,2,3)与第二组(4,5,6)的总重量:
若前两组重量相等,则假币在第三组中,比较第三组中的两枚硬币找出假币。
若前两组重量不相等,则假币在前两组中,跳转到 Step 1,继续在前两组中比较,把 6 枚硬币分成三组,按照上述方法比较,直至找到假币。
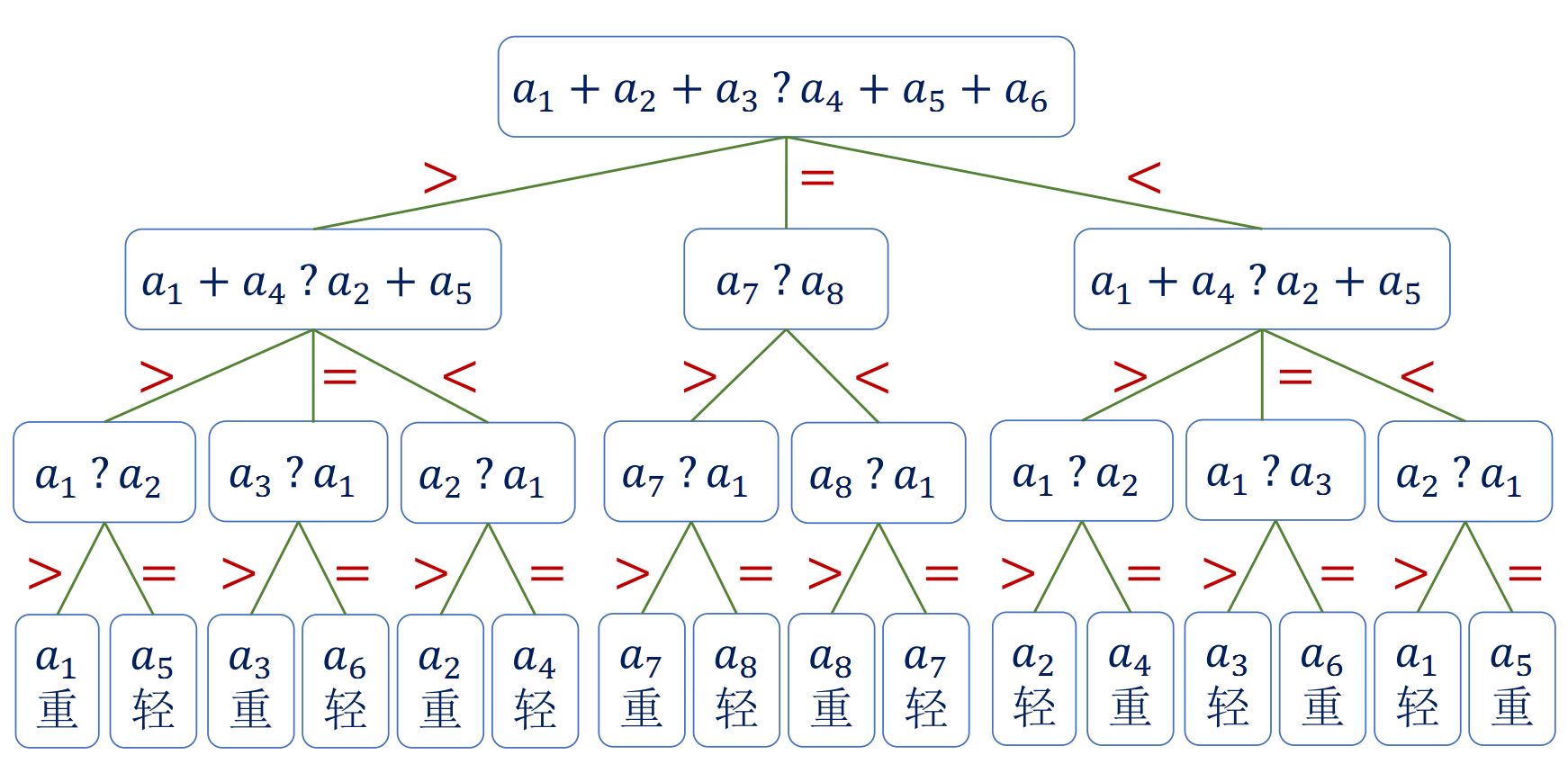
- 说明
总共 16 种情况,可能是 8 个硬币中的任意一个轻或重。
当 \(a_1 + a_2 + a_3 \neq a_4 + a_5 + a_6\) 且 \(a_1 + a_4 \neq a_2 + a_5\) ,则 \(a_3 = a_6\) ,这两枚硬币是正常的。
- 推广:\(n\) 枚硬币(以下方法非最优)
\(n\) 为偶数,均分两半,比较这两部分硬币的重量:若两部分的硬币重量相等,说明两部分都是真币; 若是不相等,说明假币在这两部分中,再细分成几个部分,递归调用该方法继续比较,直至找到假币为止。
\(n\) 为奇数,空出第一个,把剩下硬币均分两半,按偶数方法比较:如果两部分重量相等,再判断空出的第一枚硬币是否是假币; 如果两部分重量不相等,再细分成几个部分,递归调用该方法继续比较,直至找到假币为止。
14.3. 101 硬币问题
- 描述
存在一个硬币重量不一样,只需要判断该硬币是轻还是重,不需要找到该硬币是确切哪一个:只需要两次称量。
- 方案一
将硬币按 A 组(50)、B 组(50)、C 组(1)分组,先比较 A、B 两组:
若 A = B,则 C 为假币,再用 A 或 B 中任一个硬币与 C 比,C 重则假币重,C 轻则假币轻。
若 A != B,则 A 或 B 中含假币,将 A 组一分为二:A1(25)、A2(25),比较 A1、A2:
若 A1 = A2,则 A 为真币,故:A>B => 假币轻;A<B => 假币重。
若 A1 != A2,则 A 含假币,故:A<B => 假币轻;A>B => 假币重。
- 方案二
将硬币按 A 组(33)、B 组(33)、C 组(35)分组,先比较 A、B 两组:
若 A = B,则 C 含假币,再用 A + B 中任意 35 个与 C 比,C 重则假币重,C 轻则假币轻。
若 A != B,则 C 为真币,再用 C 中任意 33 个与 A 比较:
若 C = A,则 A 为真币,故:A>B => 假币轻;A<B => 假币重。
若 C != A,则 A 含假币,故:A<B => 假币轻;A>B => 假币重。
14.4. 参考资料
Balance puzzle
假币问题(八枚硬币及n枚硬币)