11. 卡特兰数
11.1. 公式
卡特兰数(Catalan Number)的递推式如下:
\[\begin{split}\mathbb{C}_n &=\ \mathbb{C}_0 \mathbb{C}_{n-1} + \mathbb{C}_1 \mathbb{C}_{n-2} + \mathbb{C}_2 \mathbb{C}_{n-3} + \cdots + \mathbb{C}_{n-2} \mathbb{C}_1 + \mathbb{C}_{n-1} \mathbb{C}_0 \\
&=\ C_{2n}^n - C_{2n}^{n-1} \\
&=\ \frac{1}{n+1} C_{2n}^n \\
&=\ \frac{1}{n+1} \frac{(2n)!}{n!n!} \\
&=\ \frac{4n-2}{n+1} \mathbb{C}_{n-1} \\\end{split}\]
前几项卡特兰数是:
\[\begin{split}\mathrm{index} & : &\ 0 &,& 1 &,& 2 &,& 3 &,& 4 &,& 5 &,& 6 &,& 7 &,& 8 &,& 9 &,& 10 &,& 11 &,& 12 &,& 13 &,& 14 &,& ... \\
\mathrm{number} & : &\ 1 &,& 1 &,& 2 &,& 5 &,& 14 &,& 42 &,& 132 &,& 429 &,& 1430 &,& 4862 &,& 16796 &,& 58786 &,& 208012 &,& 742900 &,& 2674440 &,& ...\end{split}\]
11.2. 应用
卡特兰数的应用非常广泛,基本上可以转化为左右匹配的问题,解题最重要的是确定 \(n\) 的大小。
- 计算矩阵连乘的不同计算次序。
两个矩阵连乘对应 \(\mathbb{C}_1\) ,三个矩阵连乘对应 \(\mathbb{C}_2\) ,四个矩阵连乘对应 \(\mathbb{C}_3\) 。要求在任一左括号的左边,右括号的数量不多于左括号的数量。

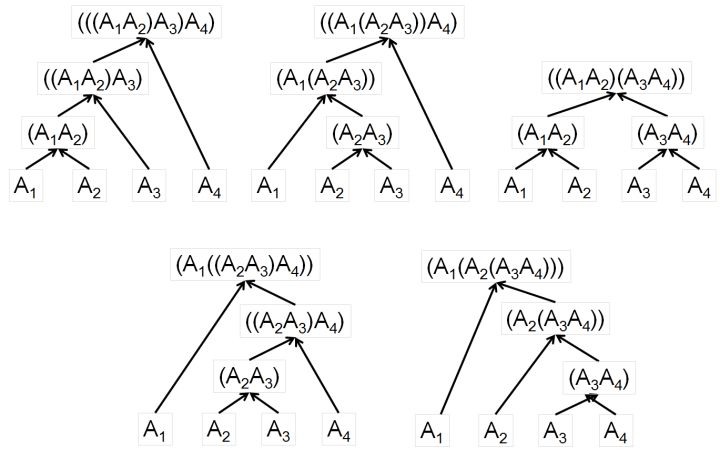
- 凸多边形的三角剖分。
正六边形的剖分对应 \(\mathbb{C}_4\) 。
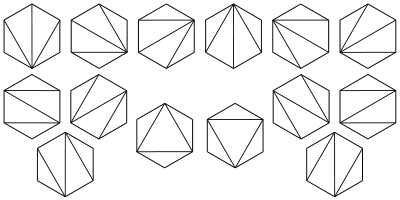
- 阶梯形的矩形剖分。
使用 \(n\) 个矩形拼成 \(n\) 阶梯形,对应 \(\mathbb{C}_n\) 。
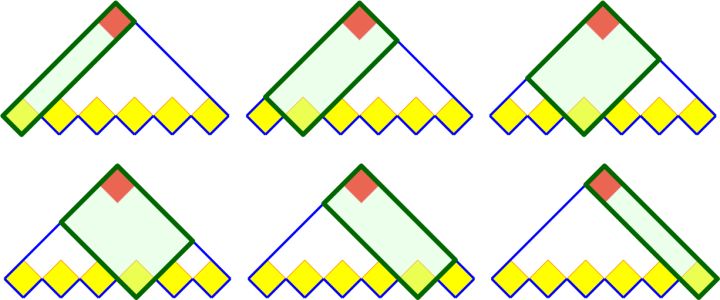
- 满位置二叉树(每个节点有0或2个子节点,且左子节点和右子节点是不同的)的计数。
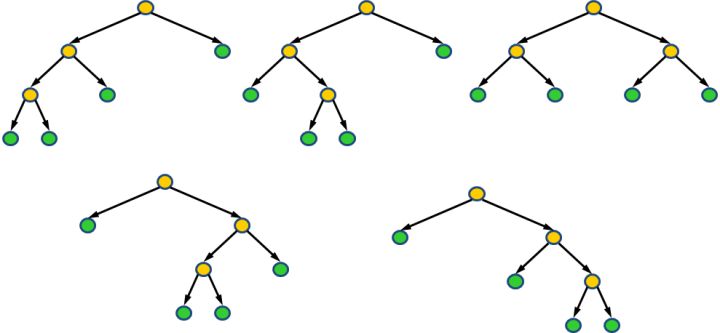
有 \(n\) 个叶子节点的满位置二叉树对应 \(\mathbb{C}_{n-1}\) 。
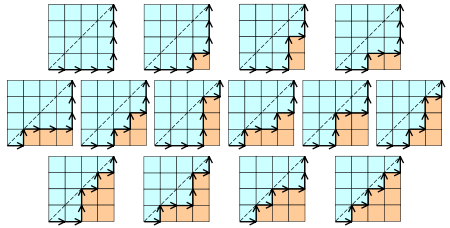
- 在 \(n \times n\) 的格子中,只在下三角行走,每次横或竖走一格,有多少种走法?
对应 \(\mathbb{C}_n\) 。要求所有走过的步数中,向右走的步数不比向上走的步数少,即 \(C_{2n}^n - C_{2n}^{n-1}\) 。
- 长度为 \(n\) 的序列的出栈方式有多少种?
对应 \(\mathbb{C}_n\) 。要求进栈的数不少于出栈的数。
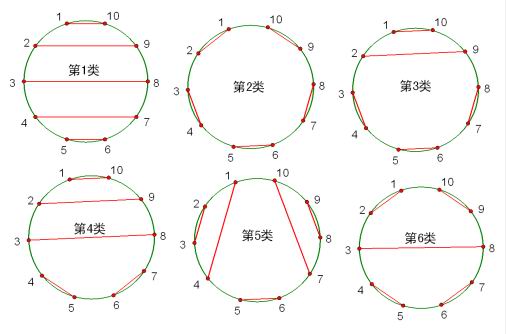
- 在圆上选择 \(2n\) 个点,将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的方法数。
对应 \(\mathbb{C}_n\) 。
- 16个人按顺序去买烧饼,其中8个人每人身上只有一张5块钱,另外8个人每人身上只有一张10块钱。烧饼5块一个,开始时烧饼店老板身上没有钱。16个顾客互相不通气,每人只买一个。这16个人共有多少种排列方法能避免找不开钱的情况出现?
对应 \(\mathbb{C}_8\) 。要求队列前方有5块钱的人数不少于有10块钱的人数。
- 12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
对应 \(\mathbb{C}_6\) 。
11.3. 参考资料
卡特兰数(Catalan number)(二)
卡特兰数
卡特兰数
卡特兰数
Catalan number